The Astrolabe Project

In Part Three we examined the obliqity arc and how to use it to find the local angle of the Sun at Noon. This week we are going to look at one use for that information, and in doing so, examine another of the sine quadrant’s advanced functions.

Links
The previous installments in this series can be found here:
Part One
Part Two
Part Three
Printable example Sine Quadrant

The Asr Lines
One of the major uses of the sine quadrant was computing the proper times for the Muslum mid-afternoon prayer, Asr[1]. To make this task easier, there are often special lines cut into the face of the quadrant.

Prayer Times
Traditionally, the times set for the 5 daily prayers required by the Muslim religion are based on the Sun’s position in the sky[2]. Of interest to us today is the mid-afternoon prayer, Asr. The period for Asr begins when the shadow of a vertical pole is equal to its noontime length plus the length of the pole; and ends when the shadow is the noontime length plus twice the length of the pole.[3]

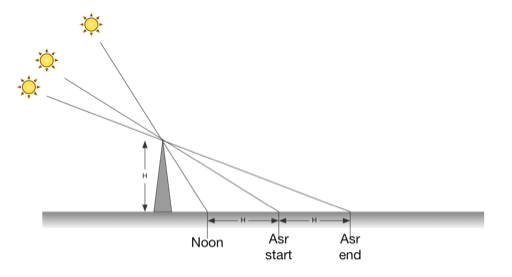
Because Asr is based on the Sun’s shadow, the times will vary depending on location, and determining the proper times for prayer must be done for each day. The sine quadrant allows the user to determine these times accurately and quickly.

If you look at the example quadrant, you will see a pair of shallow (almost straight) diagonal curves, marked in red. The curves run from the zero degree mark up to roughly the middle of the horizontal scale. The lower line is used to compute the start of Asr, the upper (often missing) allows you to compute the time for the end.

By the definition above, both times are based on the Sun’s position at Noon; This gives us one use for finding the Sun’s noontime altiude. Once the angle of the Sun at local Noon is found, it is just a matter of marking where that line crosses the two Asr curves, to determine the Sun’s angle at the beginning and end of Asr.

For example: Let’s work through finding the times for Asr for 31 degrees North (just south of the city of Alexandria, Egypt), for the 15th of February. If needed, you can go back and review [part 3] concerning the use of the obliqity arc.

First, determine the Sun’s angle at Noon:
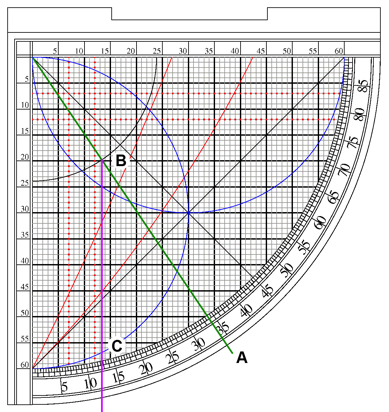
The 15th of February is 56 days after the Winter Solstice on December 21. So, remembering that the solstices are at the 90 degree mark of the angle scale, we count down 56 degrees and place the cord at 34 degrees (A). Make a note of where the cord crosses the obliqity arc (B), and follow that point down to get an angle of 13 degrees(C).

Remember that this is Winter, so the Sun is in the South and therefore the declination is negative, giving us a solar declination of -13 degrees. Using that and our known latitude we compute the Sun’s angle at noon to be:

(90-31) + -13 = 46

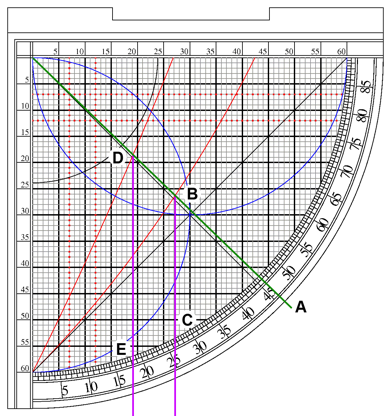
Now that we know what the Sun’s angle at Noon will be, we can determine its angle for the beginning and end of Asr very easily using the Asr lines: Place the cord on the computed Noon angle(A), and note where the cord crosses the first Asr line(B); follow this point down to the angle scale to find that the angle of the sun at the start of Asr is 26.75 degrees(C). Now note where the cord crosses the second Asr line(D), and do the same to find the angle of the Sun at the end of Asr to be 18.5 degrees(E).

After these two angles are known, it is just a matter of checking the Sun’s altitude at regular intervals to know when it is time for the prayer.

In part 5, we will examine another method of determining Asr.

Footnotes:
[1]Bir, Atilla. (2008). Principle and Use of Ottoman Sundials. Retrieved from http://www.muslimheritage.com/topics/default.cfm?ArticleID=942

[2]King, David A. A Survey of Medieval Islamic Shadow Schemes for Simple Time-Reckoning. Oriens, 32(1990), 196-197. http://www.jstor.org/stable/1580631

[3]Note: There are various schools of thought, and regional and cultural variations. The above is not definitive and is based on several sources.